Wilberforce Pendulum with Phyphox
Video tutorial (YouTube)
This apparatus allows to investigate the motion of a peculiar mass-spring oscillator named Wilberforce Pendulum, where the coupling between translational and rotational motions is very effective.
A very simple wireless device that characterizes the pendulum motion both for longitudinal and rotational oscillations, requiring no datalogger, no software: simply a common smartphone or tablet, using the free application Phyphox..

Figure 1: the pendulum
A detailed analysis of recorded data yields plots for the various components of the associated energy vs. time (kinetic and elastic, both for vertical and torsional motions, and the coupling term).
It may be shown how different initial conditions lead to different behaviors (beatings between vibration and rotation or regular exponential decay of both oscillations when one of the two fundamental modes is excited).
FFT analysis reveals the small difference between the frequencies of the two modes.
Beating is shown in Figure 2 : vertical oscillations slowly damp out while rotational oscillations increase; then the process is reversed and the energy exchange between the two modes proceeds.
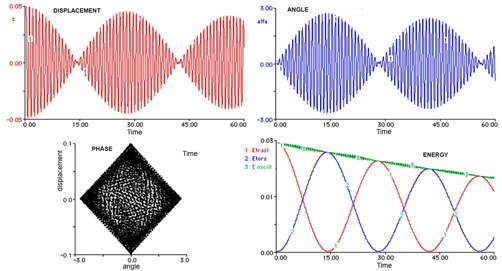
Figure 2. The beating mode
From measurements of the displacement z and of the rotation angle α we get the time evolution of the translational energy ET and of the rotational energy ER:
ET= EkT + EeT= (m/2)v2+(k/2)z2
( m = mass, v=dz/dt = velocity and k = elastic constant).
ER= EkR + EeR= 1/2 I ω 2 +(D/2) α2
( I =momentum of inertia, ω=dα/dt = angular velocity and D = torsion constant).
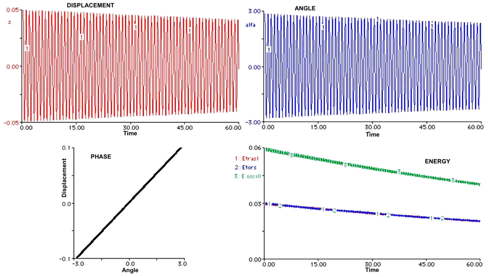
Figure 3. Fundamental mode
A suitable choice of the ratio between initial angle and displacement delete the beating and the energy is half-splitted between rotational and translational components , as shown in Figure 3.
(see: The Wilberforce pendulum: a complete analysis through RTL and modelling , Proceeding Int. GIREP Sem. , Udine, 2003)
Movie showing the 3 oscillation modes in a robotized version
Details of the 3 different modes :
Beating mode
Left fundamental mode
Right fundamental mode