L’effetto Hall è importante nello studio delle caratteristiche dei materiali perchè permette di misurare direttamente la concentrazione dei portatori di carica liberi ed il segno della loro carica, sia nei metalli che nei semiconduttori.
L’effetto Hall è essenzialmente una manifestazione della forza di Lorentz F che agisce su ogni carica elettrica q che si muova con velocità v in un campo magnetico B. Nei metalli la corrente elettrica è trasportata solo da elettroni. Nei semiconduttori invece i portatori di carica elettrica possono essere sia elettroni che lacune.
Consideriamo un tratto di conduttore di forma parallelepipeda (figura 1) immerso in un campo magnetico B uniforme diretto secondo l’asse z, percorso da una corrente elettrica di intensità Ix secondo x.
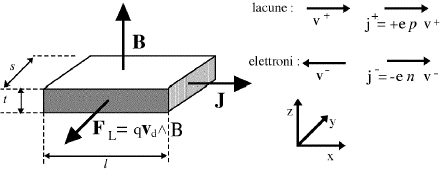
Figura 1 : Geometria dell’effetto Hall: la forza di Lorentz FL sulle cariche in moto si sviluppa nella direzione indicata dalla freccia (indipendentemente dal segno della carica)
Gli elettroni acquistano una velocità di deriva vd = -μEx sotto l’effetto del campo elettrico Ex . La forza di Lorentz FL = q vd B, agisce sugli elettroni nel verso delle y negative e quindi essi tendono ad accumularsi sulla faccia del campione perpendicolare all’asse y e posta verso chi guarda la figura 1.Questo accumulo di cariche porta alla formazione di una differenza di potenziale VH fra le due facce del campione , e quindi di un campo elettrico EH (campo di Hall) tale che la forza elettrica qEH sia uguale ed opposta alla forza di Lorentz: EH = vd B.
Conviene definire il coefficiente di Hall come RH = EH/(JB), ed è facile mostrare che vale la relazione
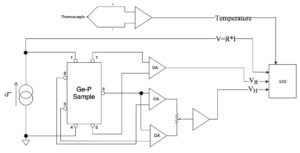
Figura 2 : Schema a blocchi dell’apparato.
Il campione di semiconduttore è posto entro una scatola di rame che può essere inserita fra le espansioni polari di un magnete. Un riscaldatore a resistenza avvolto su un cilindro di alluminio alla base del portacampione, ed un dito freddo eventualmente immerso in un bagno di azoto liquido entro il dewar, consentono di variare la temperatura nell’intervallo tra 150 K e 450 K. Il riscaldatore viene acceso manualmente eviene spento automaticamente quando la temperatura del campione supera 175 °C.
Un termometro a termocoppia, tramite un convertitore AD8495, consente di registrare il valore della temperatura insieme ai valori della tensione di Hall Vh e della resistenza R, tramite una interfaccia collegata ad un Personal Computer.
Sul campione sono saldati 7 fili nella configurazione mostrata in figura 2.
I contatti 7 e 5 servono per misurare la d.d.p. V=RI ai capi del campione in modo da poter ottenere la resistenza elettrica R. I contatti 1 e 4 servono a far passare la corrente prodotta dal circuito generatore di corrente costante.
La tensione di Hall è prelevata tra il contatto 6 e il cursore del potenziometro P che serve a bilanciare il segnale per B=0.
Un microprocessore nella scatola di controllo calcola la temperatura del campione (mediante un polinomio di interpolazione dei valori della f.e.m della termocoppia K forniti dalle tabelle NIST) e la resistenza (mediante il valore misurato della corrente di polarizzazione).
La corrente di polarizzazione ei guadagni dei due canali Vh e Vr possono essere scelti da pannello frontale e tutti i valori misurati sono mostrati in un display LCD .
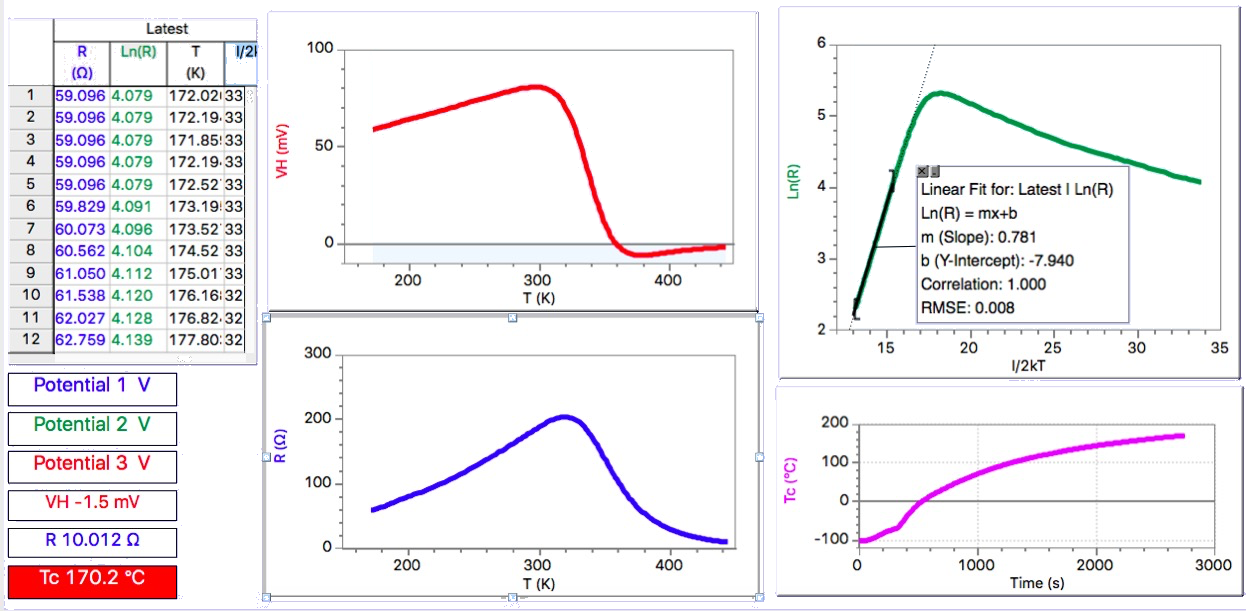
Un esempio dei risultati di una misura, in un campione polarizzato con corrente di 10 mA ed immerso in un campo di 0.4T, è riportato in figura 3.

Gaussmetro integrato

